眼观六路，耳听八方，还要上知天文，下知地理。没错，这说的就是A股散户的选股过程。选基金的道理也是一样，需要综合考量很多因素。选股也好，选基也罢，最终选的其实就是一个最优组合，即应该追求风险最小化还是收益最大化?风险和收益之间该如何权衡?本期排排君将为大家揭开建仓基金组合的秘密。

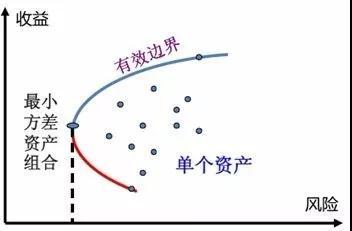
　　说到最优组合，很多投资者首先想到上期排排君说的马科维兹的均值-方差模型。

　　来源：网络

　　均值-方差模型的主要作用是选出那些在特定风险下收益最大的资产，或特定收益下风险最小的资产。但仔细想想你会发现，均值-方差模型并没有综合考虑风险与收益两者的因素，而在选基进入投资组合时仅考虑单一因素是不行的。

　　举个栗子，排排君是一位风险厌恶型投资者，投资风格属于保守型。那么根据均值-方差模型，排排君首要考虑的就是规避风险，其次才是寻找在这个风险水平下收益最大化的投资资产。

　　假如，此时市场上有两种基金供排排君选择，A基金有5%的亏损风险，但有8%的概率获取收益;而B基金有8%的亏损风险，但有15%的概率获取收益。作为保守型投资者的排排君，肯定会倾向于选择风险更低的A基金。但实际上，从理性投资角度来看，B基金的风险/收益比，比A基金更高的，即A的风险收益比为5/8=0.625，而8/15=0.533。就像咱们去购物，同样两件羽绒服，一件涨价50，但保暖性可以提升50%;另一件涨价60，保暖性可以提升80%，显然选择后者更划算。

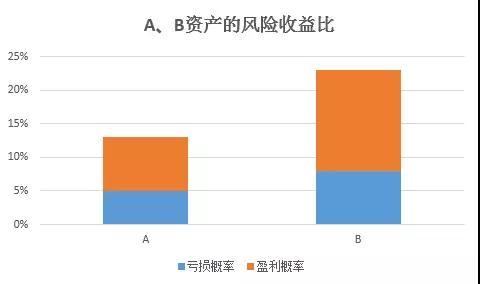
　　如上图，如果将A和B看成是商品的话，B的性价比高于A。很明显，那些保守型投资者会因为太过于注重风险性，而错过了一次获得更高收益的机会。

　　可以看出，无论是从风险角度还是收益角度，均值-方差模型都仅考虑了单方面因素，用这种方法，你只能找到了最适合你的基金组合，但这不一定是最优的。

　　卖了这么久的关子，想必很多读者已经不耐烦了。别急，这次要闪亮登场的就是综合考量风险和收益的选基经典指标——夏普比率。

　　排排君在《私募学院第5课：金融小白挑选私募基金的正确姿势!》中提到过，夏普比率是衡量私募基金风险的指标之一，比如某只基金的夏普比率是2，这意味着它所投资的股票或债券等每波动1块钱(即承担一个单位的风险)，会给该基金带来2块钱(即获得相应的单位收益)的收益。

　　其计算公式为：夏普比率=(投资组合的预期报酬率-无风险利率)/投资组合的标准差。

　　比如，一年期国债收益率是3%(咱们一般用1年期国债收益率视为无风险利率)，基金组合预期回报是20%，组合的标准差是5%，那么夏普比率则为(20%-3%)/ 5% = 3.4 ，也就是说你的基金组合每承担1个单位的风险，就能为基金组合带来3.4个单位的收益。

　　夏普比率与均值-方差模型的不同之处在于，夏普比率的本质是尽可能用最小的风险来换取最大的回报。就有点类似于排排君在第一个例子中所提到的“性价比”，而夏普比率就是基金们的性价比，可以说它是一个综合考虑投资组合风险和收益两个因素的指标，这对于成熟的投资者来筛选最优的基金是非常有必要的。

　　但需要注意的是，夏普比率并没有一个固定的绝对基准值，它的值是相对而言的。所以，我们只需要横向对比不同基金的夏普比率即可，数值越高就意味着你每承担1个单位风险所获取的收益更高，这只基的“性价比”也就越高。

　　不过，咱们在基金组合建仓时也应该注意：我每往投资组合中增加1只基金，是否会提高夏普比率?也就是说能增加多少单位的净风险收益比。如果能，说明这个基金组合带来的收益提高比带来的波动性的提高要大，投资组合正朝着最优的组合靠拢。如果不能，说明每增加1只基金带来的净风险收益比的边际效益在递减，夏普比率值已趋于极限。此时也差不多是我们完成建仓之时。